As a budding front-end developer, one of my key focus areas is understanding and internalizing algorithms and data structures. I often find it challenging to recall and reproduce algorithms that I studied some time ago. The knowledge seems to fade away, replaced by more recent learning material.

This led me to ponder if there might be a method to effectively “retrieve” an algorithm from my memory when required. Could there be a mental anchor that could trigger the knowledge I once acquired?

An idea that emerged was the use of metaphors, a technique I used extensively while learning English. I decided to adapt this approach to the realm of algorithms.

A while ago, I spent considerable time studying linked lists (traversing, reversing, merging, and so forth). I thought I grasped it pretty well. However, when I attempted to recall and write the algorithm for merging two linked lists recently, it felt as though I had never studied it before. This was particularly true for the recursive implementation.

class Node {
  constructor(value) {
    this.key = value;
    this.next = null;
  }
}

const a = new Node('A');
const b = new Node('B');
const c = new Node('C');

a.next = b;
b.next = c;

const q = new Node('Q');
const r = new Node('R');

q.next = r;

const zipLinkedLists = (head1, head2) => {
  if (!head1 && !head2) return null;

  if (!head2) return head1;

  if (!head1) return head2;

  const nextOne = head1.next; 

  const nextTwo = head2.next; 

  head1.next = head2; 

  head2.next = zipLinkedLists(nextOne, nextTwo); 

  return head1; 
};

Even after an hour of trying to reproduce the algorithm from memory, I had to give up and consult my notes. This left me more perplexed.

How does it all end up in head1?

How does the alternation pattern work, considering we’re always repeating the same steps?

I first tackled this by breaking it down step by step using an example.

/*

Iteration 1
h1 = a -> b -> c -> null
h2 = q  -> r -> null

n1 = b -> c -> null
n2 = r -> null

h1.next = h2   =>   h1 = a -> q -> r -> null
h2.next = zip(b -> c -> null, r -> null)   =>    h2 = q -> zip(b -> c -> null, q -> null)   =>   h1 = a -> q -> zip(b -> c -> null, q -> null)   <=   b -> r -> c -> null
=> h2 = q -> b -> r -> c -> null
=> h1 = a -> q -> b -> r -> c -> null

Iteration 2
h1 = b -> c -> null
h2 = r -> null

n1 = c -> null
n2 = null

h1.next = h2   =>   h1 = b -> r -> null
h2.next = zip(c -> null, null)   =>   h2 => r -> zip(c -> null, null)    =>   h1 => b -> r -> zip(c -> null, null)   <=   c -> null

=> h2 = r -> c -> null
=> h1 = b -> r -> c -> null

Iteration3
h1 = c -> null
h2 = null

return c -> null

*/

While this method helped, I knew the knowledge would only stick around for a few days. At that point, I’d been toying with the metaphor idea. What if I could find a metaphor for the recursive algorithm? That’s when the idea of train carriages on different tracks and a giant crane moving them struck me.

First, I visualized the idea with a sketch.

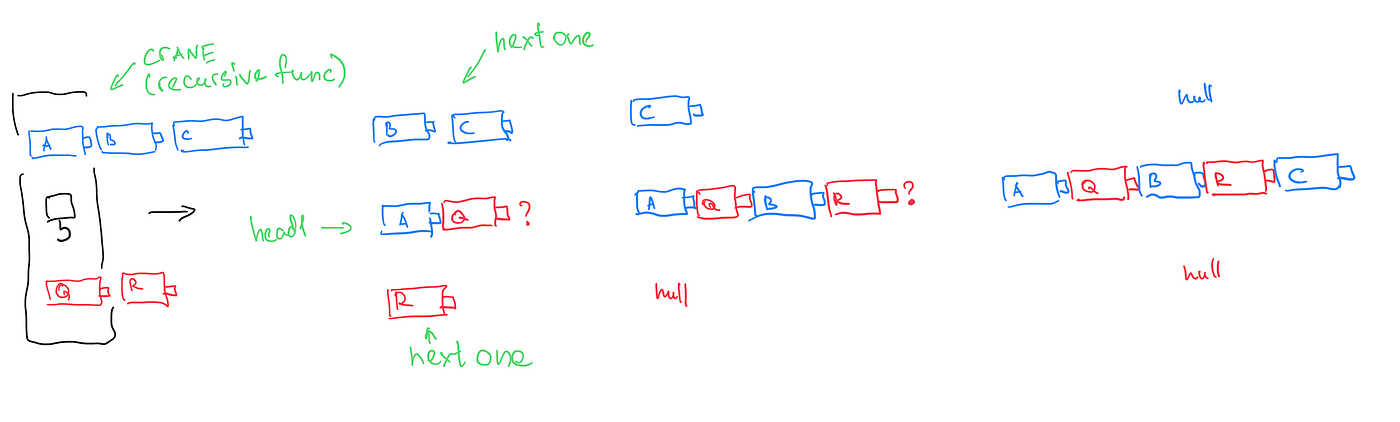
A Giant Magic Crane and Carriages

Imagine we have two train tracks. Track 1 has carriages labeled A, B, and C, while Track 2 has carriages labeled Q and R. Our task is to move the carriages onto Track 3 and link them alternately: A → Q → B → R → C.

We have at our disposal a Giant Magic Crane (our recursive function) to shift the carriages from the two tracks onto Track 3.

The crane’s limitation is that it can only connect two carriages from different tracks at a time.

However, its magic lies in its ability to create copies of itself. These copies handle the next pair of carriages, while the original Giant Magic Crane awaits the results from the newest Copy Magic Crane.

All the Magic Cranes wait until the very last copy completes its work.

Step 1

The Giant Crane takes the initiative by picking up the first carriage from Track 1 and the first carriage from Track 2, promptly placing and connecting them on Track 3.

Track 3: A → Q

Track 1: B → C

Track 2: R → null

Following this, the Giant Crane manifests a Copy Giant Crane to carry on the task, allowing the Giant Crane to pause its work and await the return of the Copy Giant Crane with more carriages from further down the line.

Step 2

Moving to the next set of carriages, the Copy Giant Crane scoops up the subsequent carriage from Track 1 and Track 2 and efficiently places them onto Track 3, connecting them to form a sequence.

This gives rise to an alternating pattern: at each juncture, the next carriage from Track 1 is followed by the carriage from Track 2.

However, at this stage, the two pairs remain disjointed. The Copy Giant Crane operates within its realm, unable to deliver its pair to the predecessor Giant Crane due to the remaining carriages that still require attention.

Track 3: A → Q, B → R (unconnected: A → Q is with the original Giant Crane, and B → R is with its copy)

Track 1: C

Track 2: null

Thus, the Copy Giant Crane conjures another Copy Giant Crane to continue the task.

Step 3, Step 4…

The newest member of the Giant Crane brigade carries on the work, producing more pairs of carriages and generating more crane copies. This process continues until there are no carriages left or there are remaining carriages on either Track 1 or Track 2.

Track 3: A → Q, B → R, C

Track 1: null

Track 2: null

Returning to the bigger task

Upon reaching a state where no more carriages are available on the tracks or when carriages are remaining on just one of the tracks, the final Giant Crane relays its current carriage load to the preceding Copy Giant Crane (null or the leftover carriages on either Track 1 or Track 2), then it vanishes.

Return C

The preceding Copy Giant Crane joins its pair with what it obtained from its clone, shifts the extended line of carriages to its originator and likewise dissipates.

Connect C to B → R: B → R → C

Return B → R → C

This cycle continues until all carriages are connected on Track 3, culminating with the original Giant Magic Crane linking the extended line of carriages received from its clones to its initial pair.

Connect B → R → C to A → Q: A → Q → B → R → C

Return A → Q → B → R → C

The END.

While I’m still evaluating how effective this approach is, it certainly gives me hope. I’ve created a simple spaced repetition plan in Notion to assist with my revisions.

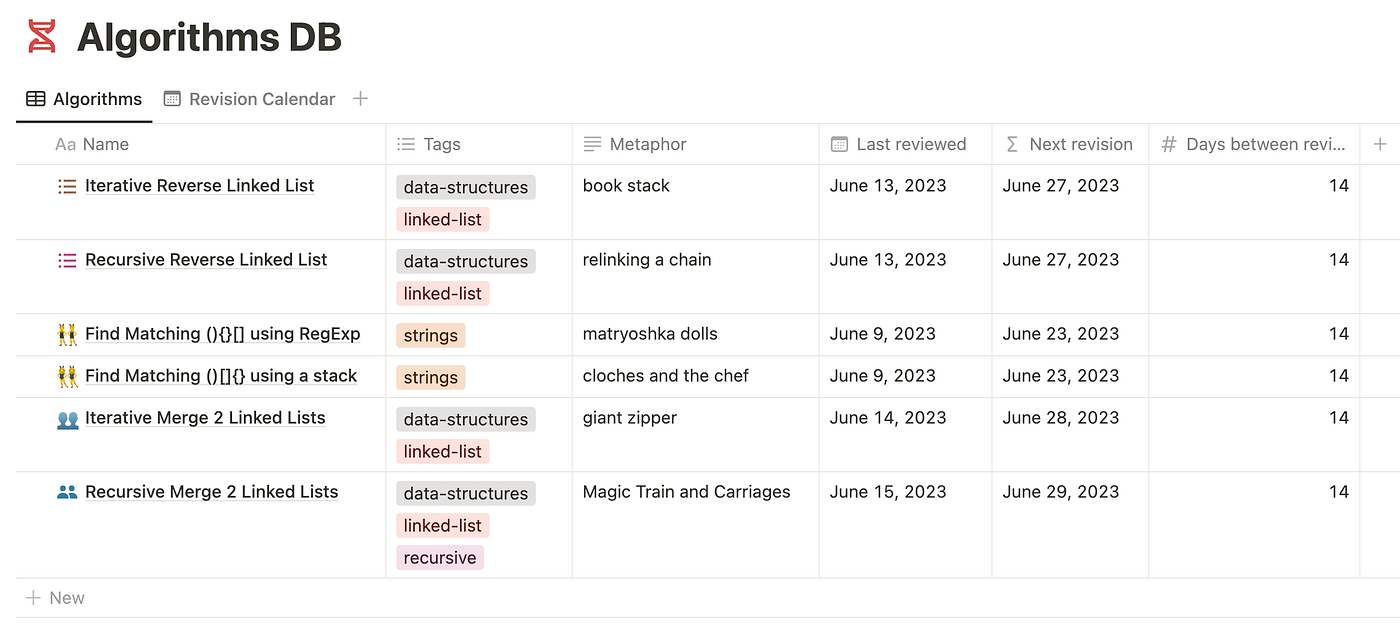
When it’s time to revise, I will attempt to reproduce an algorithm based on its associated metaphor. If nothing else, it will surely be a fun exercise! 😀

If this approach aids others in their learning journey, I would be happy. If you have suggestions to improve this metaphor, or if you have your tales of how you mastered algorithms, I would be thrilled to hear them.